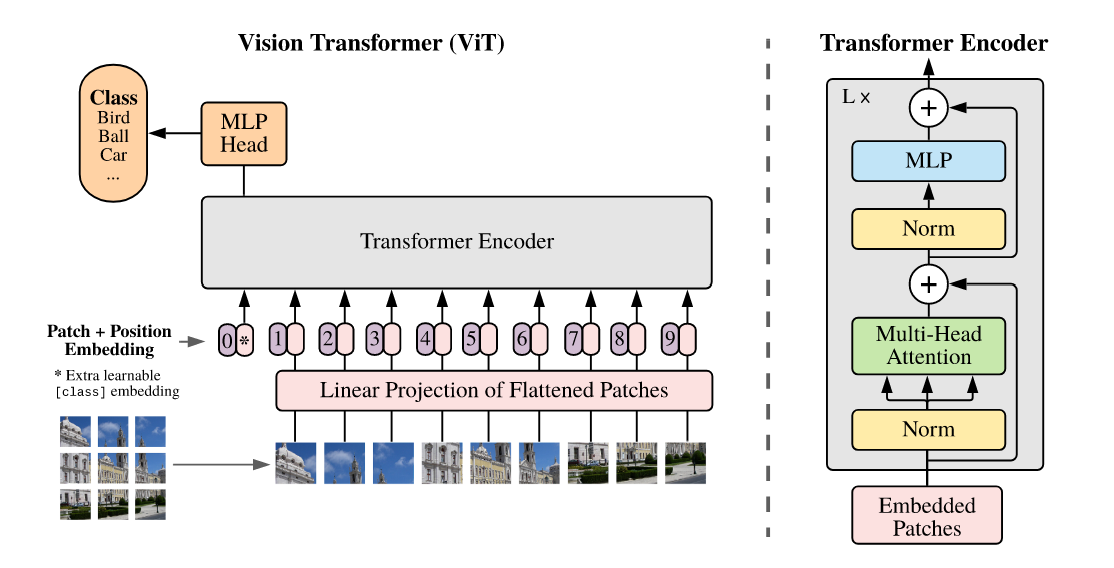
DETR(Detection Transformer)笔记

DETR (Detection Transformer)

---

1. 摘要

把目标检测的任务看成集合预测的问题.DETR 提出了新的目标函数,通过二分图匹配的方式,强制模型输出一组独一无二的预测,理想状态只输出一个框,进一步移除候选框生成与启发式后处理(如 NMS)这类额外模块.还提出了使用 Transformer encoder–decoder 的架构.在 Transformer,需要另外输入 learnable object query(类似于 anchor),DETR 可以把 object query 和全局图像信息结合在一起,通过注意力操作直接输出最终的预测框.这让训练与部署路径更统一,超参数更少.

优点:硬件支持 CNN 和 Transformer,就能支持 DETR;且非常容易拓展到其他任务.

2. 导言

2.1 问题背景(集合预测与后处理)

端到端意义:DETR 出现之前,目标检测领域很少有端到端的方法,但部分方法至少最后需要一个后处理的操作,NMS (non-maximum suppression),非极大值抑制.大部分方法都会生成很多预测框,就需要 NMS 去除.如果有 NMS,模型调参就会比较复杂,部署困难.

DETR 既不需要 proposal,也不需要 anchor,直接利用 Transformer,把目标检测看成集合预测,不会输出那么多冗余的框.

集合预测问题.大多数好用的目标检测器都用间接的方式处理集合预测问题(proposal,anchor$\cdots$),性能受限于后处理操作.DETR 提出直接的端到端方案来解决集合预测问题.

2.2 训练流程

1. 特征提取(CNN/Backbone):输入图像 → 提取卷积特征(压缩空间,保留语义,多尺度可选),并拉直为序列;
2. 全局编码(Transformer Encoder):多层自注意力融合空间上下文,形成全局记忆表征;
3. 查询解码(Transformer Decoder + Object Queries):固定数量可学习查询(实例槽位)与全局特征交互,生成候选实例嵌入;
4. 集合匹配与损失(Hungarian):一一匹配,计算分类 + L1 + GIoU 组合损失并反向传播.

要点回顾（2.1 节）

• DETR 把检测视为集合预测，输出固定数量的预测并通过一一匹配去除冗余；
• 匈牙利匹配把分类与框回归的损失作为 cost 填入损失矩阵，求最优一一匹配；
• 端到端训练的好处是减少后处理（例如 NMS）相关超参与复杂度。

2.3 推理流程

1. 特征提取(同训练);
2. 全局编码(同训练);
3. 查询解码(同训练,固定查询数保证输出上界);
4. 置信度筛选(阈值,如 > 0.7),直接输出结果(无需 NMS).

由此可见,DETR 在训练与推理阶段都不需要 anchor 生成,也不依赖 NMS 去冗余.

2.4 经验与现象

DETR 尤其对大物体表现较好(可能得益于 Transformer 的全局长程建模能力),在小物体上表现一般(局部细粒度可能不及专门的 FPN/多尺度方案).

一个常见问题是训练收敛较慢,需要更多 epoch;但换来的是后处理与调参复杂度显著降低(没有 NMS/Anchor 尺度/IoU 阈值等附加超参).

3. 相关工作

我们重点着眼于目标检测的部分

大部分目标检测器都是根据已有的初始猜测去做预测(proposal,anchor),例如:

• Faster R-CNN:两阶段结构,RPN 生成 proposal,再分类与回归,依赖 NMS;
• YOLO 系列:密集网格/锚点回归,速度快但早期版本对小目标与密集场景较敏感;
• RetinaNet:单阶段 anchor-based,提出 Focal Loss 缓解前景/背景不平衡;
  这些方法仍有冗余预测与后处理.

1. Set-based loss:可学习的 NMS 方法或关系网络,尝试利用自注意力处理物体间关系,力求独一无二的预测,从而不需要后处理;但性能普遍偏低,难以与主流方案竞争.

2. Recurrent detector:早期多用 RNN,自回归导致时效性与性能受限.DETR 采用 Transformer 的 encoder–decoder,并行处理所有查询,效率更高.

最主要的原因:使用 Transformer(神中神).

4. DETR 主体部分

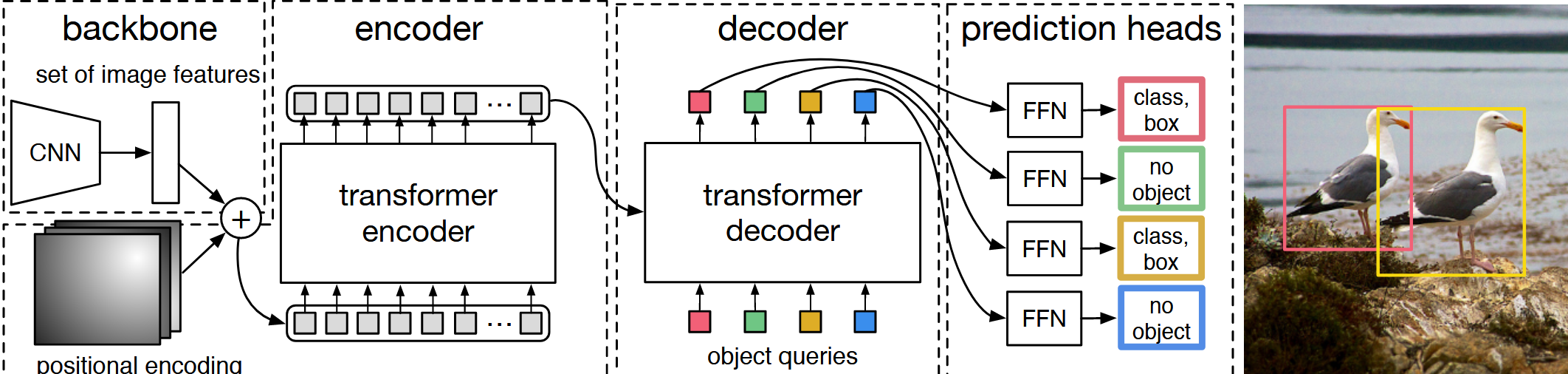
4.1 集合预测动机

DETR 输出一个固定大小的集合(n = 100),通常多于一张图片中的物体个数.固定长度的输出便于并行与张量化,且通过后续一一匹配与注意力抑制冗余,避免传统方法里”多→删”的后处理路径.一张图片的 GT 的 bounding box 可能只有几个,如何匹配并计算 loss?可以用二分图匹配解决.

4.2 匈牙利(二分图)匹配例子

可以理解为:如何分配工人完成任务,使得总成本最小.

假如说现在我有3个工人a,b,c,要去完成3个工作x,y,z

	x	y	z
a
b
c

每个矩阵里有各工人完成这些任务所需要的时间(或者是所需要的钱),这个矩阵就叫做 cost matrix(损失矩阵).

最优二分图匹配的意思就是最后能找到一个唯一解,给每个人分配最合适的工作,使总成本最低(Hungarian 算法复杂度约 O(n^3)).

可以通过 SciPy 包里的 linear_sum_assignment 函数完成,输入 cost matrix,输出最优排列(训练时可在批量维度并行).

在目标检测里,同样是二分图匹配问题.可以把 a,b,c 看作 100 个预测框,把 x,y,z 看作 GT 框.

4.3 损失函数组成

那么对于目标检测来说,cost matrix 中该放什么?从名字就可知应该放 cost,而 cost 本质上就是 loss.对于目标检测,loss 可以这么算:

$$ext{cost}(i, j) = -\mathbf{1}_{\{c_i \ne \varnothing\}}\;\hat{p}_j(c_i) \; + \; \mathbf{1}_{\{c_i \ne \varnothing\}}\;\mathcal{L}_{\text{box}}(b_i,\;\hat b_j)$$

前半部分表示分类的 loss,后半部分表示边界框的准确度.遍历所有预测框,与 GT 的框计算上述两种 loss,并将该 loss 放入 cost matrix.一旦有了 cost,就可以直接用 SciPy 的 linear_sum_assignment 求最优匹配.实践中常对分类与框回归设置权重(λ_cls, λ_bbox, λ_giou)以平衡梯度贡献.

最后的匹配后整体目标函数如下:

$$\mathcal{L}_{\text{Hungarian}}(y, \hat{y}) = \sum_{i=1}^N \left[ -\log \hat{p}_{\hat{\sigma}(i)}(c_i) \;+ \;\mathbf{1}_{\{c_i \ne \varnothing\}}\;\mathcal{L}_{\text{box}}\big(b_i,\;\hat b_{\hat\sigma(i)}\big) \right]$$

在 DETR 中,作者做了两个与常规目标检测不同的设置.第一:分类 loss 通常用 $\log$,但作者为了让两类 loss 的量纲更接近,尝试去掉 $\log$;

第二:在 bounding box 回归上,早期工作常用一个 $L_1$ loss,但 $L_1$ 与框大小相关,框越大 loss 越大.DETR 的全局特征容易给大目标出大框,可能使 loss 偏大,不利优化.因此不仅使用 $L_1$,还加入 Generalized IoU(GIoU)loss(与框尺度无关),将两种 loss 组合为最终的 box loss(互补:L1 捕捉坐标偏差,GIoU 衡量空间重叠质量).

GIoU 简介

GIoU（Generalized Intersection over Union，广义交并比）是在传统 IoU 基础上的一个改进，目的是在预测框与真实框不相交时仍能给出有意义的度量并产生可用的梯度信号，从而帮助优化器继续学习如何把预测框移动到目标位置。

先回顾 IoU 的定义：若 $A$ 和 $B$ 分别表示预测框与真实框，则

$$\mathrm{IoU}(A,B)=\frac{|A\cap B|}{|A\cup B|},$$

取值范围为 $[0,1]$。当两个框没有重叠时，$\mathrm{IoU}=0$，这时仅依赖 IoU 的损失难以为模型提供改进方向（梯度信息弱或为 0）。

GIoU 的思想是：在 IoU 的基础上再引入一个关于两个框相对位置的补偿项。令 $C$ 为包含 $A$ 与 $B$ 的最小外接矩形（即把两框都包住的最小矩形），则 GIoU 定义为：

$$\mathrm{GIoU}(A,B)=\mathrm{IoU}(A,B)-\frac{|C|-|A\cup B|}{|C|}.$$

第二项的物理含义可以这样理解：$|C|-|A\cup B|$ 表示外接矩形中空白区域的面积，除以 $|C|$ 得到一个归一化的空白比例。这个比值越大，说明两个框彼此远离（或重叠很少），GIoU 就会相应地减小，给出更强的惩罚。

常用的 GIoU 损失写作：

$$\mathcal{L}_{\mathrm{GIoU}}(A,B)=1-\mathrm{GIoU}(A,B)$$

取值上，GIoU 的范围比 IoU 更大，可以是负值（当外接矩形中空白区域占比较大时），因此 GIoU 在没有重叠时仍会产生可优化的梯度。

为何将 GIoU 与 $L_1$（或 $L_1$+归一化坐标误差）结合使用？直观上：

• $L_1$（坐标级回归）直接度量预测框中心与宽高的偏差，能精确告诉优化器每个坐标应该朝哪个方向移动；
• GIoU 捕捉的是“重叠质量”和相对空间关系，尤其在两个框不重合或部分重合时给出全局性的结构性惩罚。

两者结合的好处是互补：$L_1$ 提供局部坐标修正，GIoU 提供全局重叠/布局信息，合用能加速收敛并提高最终定位精度。

实现细节与注意点：

• 计算 IoU/GIoU 时通常需要把中心坐标/宽高格式 $[c_x,c_y,w,h]$ 转为角点格式 $[x_{min},y_{min},x_{max},y_{max}]$；
• GIoU 在数值上可能为负，训练时与分类 loss、$L_1$ 加权相加（例如 DETR 使用的权重 λ_bbox、λ_giou），以平衡不同损失项的尺度；
• GIoU 更关注空间重叠而对尺度变化不敏感（scale-invariant），这使得它在不同尺寸目标上表现更稳定。

小结：把 GIoU 看作在 IoU 上加了一层“远近惩罚”，当两个框远离时，GIoU 会给出更强的惩罚，从而为优化器提供有方向性的梯度；与 $L_1$ 结合则能兼顾位置精度与重叠质量。

L1 损失简介

L1 损失（也称为曼哈顿距离或绝对差损失）在边界框回归中是最直接、最常用的坐标级别误差度量之一。若用向量 $b=[c_x,c_y,w,h]$ 表示一个框，预测框为 $\hat b=[\hat c_x,\hat c_y,\hat w,\hat h]$，则常用的 L1 损失可以写作：

$$\mathcal{L}_{L_1}(b,\hat b)=\|b-\hat b\|_1=\sum_{t\in\{c_x,c_y,w,h\}}|b_t-\hat b_t|.$$

直观理解：L1 把每个坐标的绝对偏差相加，告诉优化器“每个坐标应向哪个方向以及大致多少量移动”。因此 L1 信号局部且直接，适合微观层面的坐标修正。

注意事项:

• 归一化：通常用归一化后的坐标（例如相对于图片宽高，或将中心坐标/宽高归一到 [0,1]），以避免不同图像尺寸带来的绝对量纲差异。
• 尺度敏感：L1 对框的尺度敏感——相同的相对误差在大框上会产生更大的绝对 L1 值，这也是为什么单独使用 L1 有时会偏向优化大框。
• 变体：在实际训练中常用 Smooth L1（Huber loss）来兼顾对离群点的鲁棒性；也有人对坐标分量做加权或归一处理以平衡不同项。

与 GIoU 的互补性（一句话总结）：L1 给出精确的坐标级修正方向，GIoU 给出整体的重叠/位置质量评价，两者合用能同时提供局部（坐标）和全局（重叠）两类有用梯度，利于定位收敛和最终精度。

4.4 模型架构概览

以作者在代码库里的例子:

输入图片的大小是 $3 \times 800 \times 1066$(3 指 RGB).
第一步通过卷积网络得到特征.走到最后一层 Conv5 时,会得到 $2048 \times 25 \times 34$ 的特征;再做一次 $1 \times 1$ 的降维操作,把 2048 变成 256.因此从卷积神经网络出来的特征维度是 $256 \times 25 \times 34$.

接下来进入 Transformer.Transformer 没有位置信息,因此要加入位置编码.在 DETR 中加入一个固定的位置编码,维度同样是 $256 \times 25 \times 34$.

将两者相加后作为 Transformer 的输入,并拉直为 $850 \times 256$.其中 850 是序列长度,256 是 Transformer 的 hidden dimension.不论经过多少个 Transformer encoder block,输出都是 $850 \times 256$.在 DETR 里,作者使用了 6 个 encoder.

然后将 encoder 的输出送入 decoder,得到框的输出.关键对象:object query —— learnable 的 positional embedding,维度为 $100 \times 256$;其中 256 与前述维度一致,100 表示最大实例槽位数.在 decoder 中进行 cross attention:每个查询与来自图像端的全局特征交互,自注意力在查询之间传递抑制/互斥信息,有助于移除冗余.同样,DETR 使用 6 层 decoder.

拿到 $100 \times 256$ 的最终特征后,接一个预测头(feed-forward network,MLP),做两个预测:

• 类别分布(COCO 为 91 类,另含”空”类用于未匹配查询);
• 边界框(中心点 x,y 与宽,高,通常归一化到 [0,1]).
  当得到这 100 个预测框后,与 GT 做最优匹配,用匈牙利算法计算目标函数,再反向传播更新模型.

4.5 细节提示

• Transformer decoder 中,第一层 decoder 可以不做 object query 的自注意力操作;
• 每个 decoder 后都加 FFN,得到检测输出并计算 loss(中间层监督有助于收敛稳定);
• 归一化边界框坐标到 [0,1] 有助于缓解尺度差异.

5. 伪代码

import torch
from torch import nn
from torchvision.models import resnet50

class DETR(nn.Module):
    def __init__(self, num_classes, hidden_dim, nheads, num_encoder_layers, num_decoder_layers):
        super().__init__()
        self.backbone = nn.Sequential(*list(resnet50(pretrained=True).children())[:-2])
        self.conv = nn.Conv2d(2048, hidden_dim, 1)
        self.transformer = nn.Transformer(hidden_dim, nheads, num_encoder_layers, num_decoder_layers)
        self.linear_class = nn.Linear(hidden_dim, num_classes + 1)
        self.linear_bbox = nn.Linear(hidden_dim, 4)
        self.query_pos = nn.Parameter(torch.rand(100, hidden_dim))
        self.row_embed = nn.Parameter(torch.rand(50, hidden_dim // 2))
        self.col_embed = nn.Parameter(torch.rand(50, hidden_dim // 2))
    
    def forward(self, inputs):
        x = self.backbone(inputs)
        h = self.conv(x)
        H, W = h.shape[-2:]
        pos = torch.cat([
            self.col_embed[:W].unsqueeze(0).repeat(H, 1, 1),
            self.row_embed[:H].unsqueeze(1).repeat(1, W, 1),
        ], dim=-1).flatten(0, 1).unsqueeze(1)
        h = self.transformer(pos + h.flatten(2).permute(2, 0, 1), self.query_pos.unsqueeze(1))
        return self.linear_class(h), self.linear_bbox(h).sigmoid()

detr = DETR(num_classes=91, hidden_dim=256, nheads=8, num_encoder_layers=6, num_decoder_layers=6)
detr.eval()
inputs = torch.randn(1, 3, 800, 1200)
logits, bboxes = detr(inputs)

注:上述伪代码仅展示核心结构骨架,未包含完整训练细节(优化器,数据增强,学习率调度,中间层监督,权重初始化等).

---

6. 参考文献

1. Carion, N., Massa, F., Synnaeve, G., Usunier, N., Kirillov, A., & Zagoruyko, S. (2020). End-to-End Object Detection with Transformers. ECCV. arXiv

好喜欢Palind这种小南梁…